Product-Item, Economic Complexity, Country Competitiveness, Hidalgo
Below we create a model that represents a country's economy based on the products it produces, and the complexity of those products. "Complexity" of both the country and products it produces will essentially be based on the number of different product types, but the chicken-egg aspect of the deeper model will be teased out of the product export raw data using the method below.
Model
The complexity of an economy is proportional to the average complexity of its products, and, vice versa, the complexity of a product is proportional to the average complexity of its producers.
We could say $m_{ij}=1$ if country $i$ makes product $j$ , and $m_{ij}=0$, otherwise, but we need a preprocessing stage first. Let's say $X_{ij}$ is exports (in dollar amounts) of product $j$ of country $i$. The Revealed Comparative Advantage of that country $i$ is
$$ RCA_{ij} = \frac{X_{ij}}{\sum_i X_{ij}} / \frac{\sum_j X_{ij}}{\sum_{i,j} X_{i,j}} $$
Then if $RCA_{ij} > 1.0$ we set $m_{ij}=1$, 0 otherwise.
The weights are $v_{ij} = m_{ij} / d_i$, $w_{ij}=m_{ij}/u_j$ where the diversification of country $i$ and the ubiquity of product $j$ are simply $d_i = \sum_j m_{ij}$, $u_j = \sum_i m_{ij}$. So if $c_i$ is the complexity of country $i$ and $p_j$ is the complexity of product $j$
$$ c_i = \alpha \sum_j v_{ij}p_j $$
$$ p_j = \beta \sum_i w_{ij} c_i $$
where $\alpha,\beta>0$. We see the chicken-egg problem here. We collect variables inside matrices $c$, $p$, $V=[v_{ij}]$ and $W=[w_{ij}]$, then $c = \alpha V p$ and $p = \beta W c$. If we subtitute second the latter in the former, $c = \alpha \beta (V^T W) c$, or the former in the latter, $p = \alpha \beta (V W^T) p$. This means the complexities of countries and products are given by an eigenvector of $V^T W$ and $V W^T$ respectively.
Code
Looking only at 2014 trade data.
import pandas as pd, zipfile
with zipfile.ZipFile('/tmp/hidalgo.zip', 'r') as z:
df = pd.read_csv(z.open('hidalgo.csv'),sep='\t')
gdp = pd.read_csv(z.open('gdp1416.csv'),sep=',',index_col=0)
hs = pd.read_csv(z.open('hs.csv'),sep='|')
hs2 = pd.read_csv(z.open('hs2.csv'),sep=',',index_col='ProductCode_x')
pd.set_option('display.max_columns', None)
print (len(df))
print (df.tail(10))
726013
year origin hs92 export_val import_val export_rca import_rca
726003 2014 ven 961610 39395.0 2026297.0 0.011 0.947
726004 2014 ven 961620 NaN 1084958.0 NaN 2.413
726005 2014 ven 961700 29666.0 1701096.0 0.005 0.495
726006 2014 ven 961800 2066.0 113839.0 0.001 0.074
726007 2014 ven 970110 210867.0 385141.0 0.004 0.014
726008 2014 ven 970190 179993.0 118881.0 0.136 0.155
726009 2014 ven 970200 976805.0 NaN 0.563 NaN
726010 2014 ven 970300 717009.0 277338.0 0.068 0.045
726011 2014 ven 970500 12723.0 NaN 0.004 NaN
726012 2014 ven 970600 NaN 2484.0 NaN 0.000
cp = df.pivot_table('export_val', index='origin', columns='hs92')
print (cp.shape)
print (len(np.unique(df.hs92)), 'products')
(220, 4858)
4858 products
denom = cp.sum(axis=1) / cp.sum().sum()
denom = cp.sum(axis=1) / cp.sum().sum()
cp2 = cp.div(cp.sum(axis=0).T)
cp2 = cp2.div(denom,axis=0)
cp2 = cp2.fillna(0)
cp2[cp2 > 1.0] = 1.0
cp2[cp2 != 1.0] = 0.0
cp3 = cp2
cp4 = cp3.div(cp3.sum(axis=1),axis=0)
cp5 = cp3.div(cp3.sum(axis=0),axis=1)
print (cp4.shape, cp5.shape)
(220, 4858) (220, 4858)
Country, Product Complexity Method using Eigenanalysis
Country ECI
import scipy.linalg as lin
print (cp4.shape)
uc,vc = lin.eig(np.dot(cp4,cp5.T))
print (vc.shape)
eci = np.array(vc)[:,1]
print (len(eci))
print (np.argmax(eci))
top_countries = cp.index[np.argsort(eci)[:10]]
print (top_countries)
(220, 4858)
(220, 220)
220
181
Index(['jpn', 'che', 'deu', 'kor', 'swe', 'xxb', 'usa', 'sgp', 'cze', 'fin'], dtype='object', name='origin')
Look at simple product sum, is the list the same?
Product PCI
Utilize sparsity,
import scipy.sparse.linalg as lin
import scipy.sparse as sps
scp4 = sps.lil_matrix(cp4)
scp5 = sps.lil_matrix(cp5)
A = scp4.T.dot(scp5)
up,vp = lin.eigs(A,k=2)
pci = np.array(vp)[:,1]
hs3 = hs2.reset_index()
hs3.columns = ['code','idx','desc1','desc2']
hs3 = hs3.set_index('code')
top_prods = cp.columns[np.argsort(pci)[:10]]
pd.set_option('expand_frame_repr', False)
top_prods2 = [str(x) for x in list(top_prods)]
#print (hs3.loc[top_prods2])
for x in top_prods2:
if x in hs3.index:
print (hs3.loc[x])
idx 884
desc1 - Other
desc2 Plants and parts of plants (including seeds an...
Name: 121190, dtype: object
idx 3132
desc1 -- Other
desc2 Wood in the rough, whether or not stripped of ...
Name: 440399, dtype: object
idx 3144
desc1 (-1995, 2007-) -- Virola, Imbuia and Balsa
desc2 Wood sawn or chipped lengthwise, sliced or pee...
Name: 440722, dtype: object
idx 3125
desc1 (-1995) Keruing, Ramin, Kapur, Teak, Jongkong,...
desc2 Wood in the rough, whether or not stripped of ...
Name: 440333, dtype: object
idx 852
desc1 - Sesamum seeds
desc2 Other oil seeds and oleaginous fruits, whether...
Name: 120740, dtype: object
idx 3008
desc1 (-2001) - - Other
desc2 Tanned or crust skins of sheep or lambs, witho...
Name: 410519, dtype: object
idx 5422
desc1 Copper waste and scrap.
desc2 Copper waste and scrap.
Name: 740400, dtype: object
Simple regression
cindex = [x.upper() for x in cp.index]
ecigdp = pd.DataFrame(eci,index=cindex)
ecigdp = ecigdp.join(gdp)
print (ecigdp.shape)
ecigdp.columns = ['eci', u'gdp2014', u'gdp2016']
ecigdp['prods'] = np.array(cp3.sum(axis=1))
ecigdp = ecigdp.dropna()
print (ecigdp.tail())
import statsmodels.formula.api as smf
results = smf.ols('np.log(gdp2014) ~ eci', data=ecigdp).fit()
print (results.rsquared_adj)
results = smf.ols('np.log(gdp2014) ~ prods', data=ecigdp).fit()
print (results.rsquared_adj)
(220, 3)
eci gdp2014 gdp2016 prods
WSM 0.025062 3761.912686 3524.649880 209.0
YEM 0.075479 679.667360 1101.117444 147.0
ZAF 0.008537 7504.295250 7627.851926 742.0
ZMB 0.048409 1622.409958 1620.823290 182.0
ZWE 0.063000 908.829980 932.548383 275.0
0.5550344026397989
0.23070167903402794
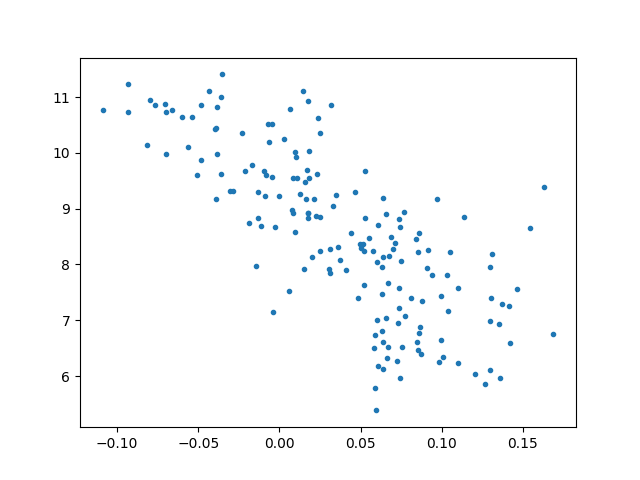
plt.plot(ecigdp.eci,np.log(ecigdp.gdp2014),'.')
plt.savefig('eci_01.png')
References