Crowd Wisdom
"At a country fair .. 800 people participated in a contest to estimate the weight of a slaughtered and dressed ox. Statistician Francis Galton observed that the median guess, 1207 pounds, was accurate within 1% of the true weight of 1198 pound". It sounds magical, a group of people seemingly throwing out numbers, and their average is close to the true measurement. How?
Humans already have built-in knowledge about the visual-look-weight connection on many items, so their guesses will be already close enough to the real thing, with plus noise. That noise is the key part. The distribution of that noise is bell-shaped (Gaussian), white noise is Gaussian with zero mean. This is important, while averaging, we also take the average of white noise, whose mean is zero. The noise disappears, we are left with a good estimate.
This technique even works internally sometimes, it is called "the wisdom of the crowd within". "[Researchers] asked participants for point estimates of continuous quantities associated with general world knowledge, such as '[w]hat percentage of the world's airports are in the United States?' [then] half of the participants were immediately asked to make a second, different guess in response to the same question [..t]he average of a participant's two guesses was more accurate than either individual guess"
We need to stress however, for standard normal noise to exist, the base has to be a domain where guessors have an expertise. That is the only way guesses are close to reality, and there is no bias one way or another.
"Can we use the same idea for policy, like millions making policy, direct democracy?"
In most policy issues regular people have no expertise. For judging the weight of something, we already have perhaps inborn, at the very least life-long experience there... During our lives we have handled, touched, carried things, so looking at an object we can make weight guesses. The estimate will have noise but it won't be far off from the truth which can be corrected statistically. Policy is not something people are engaged in daily. Which makes it a speciality.
But averaging among specialists will work.
The Mechanism of Averaging
Normal distribution is odd; it shows up everywhere. Take a group of ppl, their height dist is normal. Have someone shoot at a target, measure distance from each hit to bulls eye, dist is normal. Whenever many factors contribute to a thing, normality occurs.. bcz sums of anything (random) approaches normal. And there are many things like that in nature.
Throw a 6-sided die 1000 times (numbers below are from software generator), histogram rolls,
import random
n = 1000; b = 6
rolls = [random.randint(1,6) for i in range(b*n)]
rolls = np.array(rolls)
plt.hist(rolls,bins=6)
plt.savefig('dice2.png')
Nearly uniform (not normal), all equal chance,
But if I sum every 6 die throws and histogram,
rolls = [random.randint(1,6) for i in range(b*n)]
rolls = np.array(rolls).reshape(n,b)
s = np.sum(rolls,axis=1)
plt.hist(s,bins=12)
plt.savefig('dice1.png')
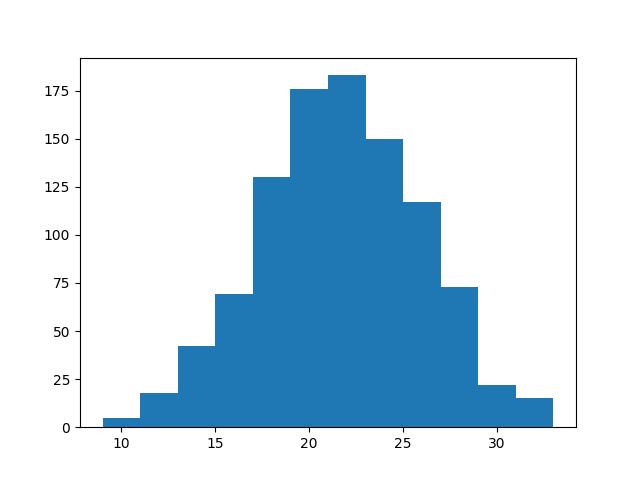
Bell shaped. Normal.
Why? Bcz more sums result in a 6 than 2. I can get 6 with 4+2,2+4,1+5,3+3,etc.. More chance to hit it. Very low, very high nums are harder. Easy sums form the bulk in the middle.
Height frequency is normal.. many factors contribute to height. Some ppl might have a fat ass, small back, others large back, skinny ass. Large or small head.. All cld lead to same height.
Note that both shooting, and weight guessing involves knowledge / skill. Good "standard" noise around bullseye means person knows how to shoot. Judging weight by naked eye we have skill in through evolution, and part of growing up. Stat ppl know this, when they apply a model to data, they determine whether "the fit" is good by looking at its mistake, its "residual" (diff between model prediction, and real data). If resid is gaussian, that's a good sign. Bad models leave patterns in data. When unskilled (or dumb) people screw up you know why. There is pattern in their muck ups (usually due to some bias).